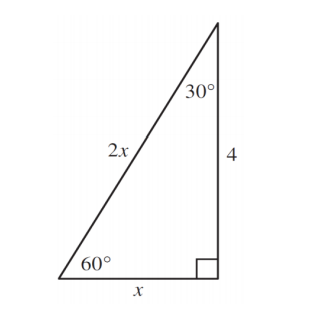
Special right triangles like the 30° 60° 90° triangle are one of the easiest problems to solve.
Whether you are looking for the hypotenuse or any of the two missing sides, you no longer have to memorize and apply lengthy formulas to find it.
You can solve any problem about 30° 60° 90° triangles as long as you know and understand their ratios.
By simply understanding their ratios, you would be able to evaluate the trigonometric functions of any angle in a 30°-60°-90° triangle without using a calculator.
Knowing the ratios would save you a lot of time in an exam because you no longer have to write long equations to find the missing information.
That being said, we would further discuss what makes a 30°-60°-90° triangle special as well as illustrate some examples to help you have a better understanding of how to solve it.
Table of Contents
What is a 30 60 90 triangle?
A 30 60 90 triangle has the following ratios:
- 1 : 2 : 3 ratios for their angles (30° 60° 90°)
- 1 : √3 : 2 ratios for their sides (x : x√3 : 2x)
You might be wondering… how did we come up with these ratios?
Well, for starters, it helps if we visualize an equilateral triangle (all of its sides are equal) and apply the Pythagorean Theorem.
If you splice the equilateral triangle by half, you now have two 30° 60° 90° triangles on both sides
Since all sides in an equilateral triangle are equal, we can conclude that AD is equal DC.
Now, let us apply the Pythagorean Theorem to find BD
Pythagorean Theorem states that a2 + b2 = c2
(BD)2 + (x2)2 = x2
BD2 + x24= x2
BD2 = x2 – x24
BD2 = 4×2-x24
BD2 = 3×24
BD = 3×2
So if the equilateral triangle would make two 30° 60° 90° triangles, it should look like this
Keep in mind that two 30° 60° 90° triangles should make an equilateral triangle, meaning all sides should be equal.
Since the lower side has been splice into two, we can conclude that it now has the smallest side when it became a single 30° 60° 90° triangle.
The hypotenuse is now twice on the smallest side.
As we illustrated below, the other missing side is now x√3
With that, we now have a ratio of 1 : √3 : 2 or x : x√3 : 2x for all sides
Things you should remember
Given that this is a special right triangle, all the statements below are also applicable to any 30° 60° 90° triangles
- As we noted above, the Pythagorean Theorem a2 + b2 = c2 is applicable and can be used in a 30° 60° 90° triangle
- Interior angles always add up to 180° (30° + 60° + 90° = 180°). Therefore, you can easily determine the missing angle simply by subtracting the sum of the two angles to 180
- The smallest and longest sides are always opposite to the smallest and largest angle (as cited above)
- Triangles with the same angle measures have the same ratio for their sides.
- A 30° 60° 90° triangle is half of an equilateral triangle, which means they are also a congruent triangle
What is the formula for the 30 60 90 triangles?
As we have said before, you no longer have to use or remember the lengthy formula for a 30° 60° 90° triangle.
You just need to identify the sides and remember the 1: √3 : 2.
Short Leg
Hypotenuse
Long Leg
How to solve the missing side?
To make this a lot easier for you, we have cited three scenarios that you might face in your exams.
You can just use the basic arithmetic method and solve any problem related to the 30° 60° 90° triangle in no time.
Always remember this ratio
- 1 : 2 : 3 ratios for their angles (30° 60° 90°)
- 1 : √3 : 2 ratios for their sides (x : x√3 : 2x)
Short Leg
If you only know the measurement of the Short Leg, then you can simply double it to find the Hypotenuse and multiply the Short Leg by the square root of 3 to find the Long Leg.
Hypotenuse
If you only know the measurement of the Hypotenuse, then you can divide it by two to get the Short Leg and then multiply the Short Leg by the square root of 3 to find the long leg.
Long Leg
If you only know the measurement of the Long Leg, then you can divide it by the square root of 3 to find the Short Leg and then double that Short Leg to find the hypotenuse.
Practice Problem
We have compiled a few practice problems about 30 60 90 triangles from different educational institution website.
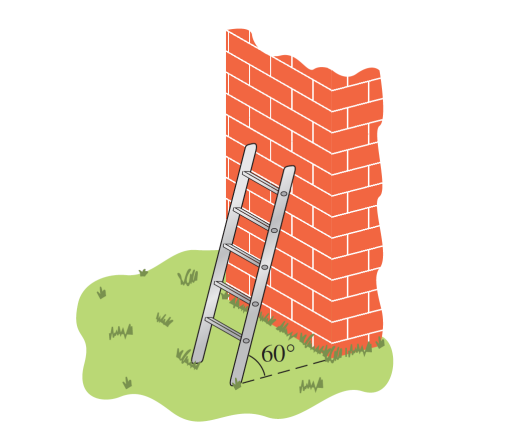
A ladder is leaning against a wall. The top of the ladder is 4 feet above the ground and the bottom of the ladder makes an angle of 60 with the ground (Figure 16). How long is the ladder, and how far from the wall is the bottom of the ladder?
Answer: The distance from the bottom of the ladder to the wall, x, is 4√3/3 feet, so the length of the ladder, 2x, must be 8√3/3 feet.
Explanation: It would be best to visualize as well as identify the given terms and missing sides. The triangle formed by the ladder, the wall, and the ground is a 30° 60° 90° triangle. If we let x represent the distance from the bottom of the ladder to the wall, then the length of the ladder can be represented by 2x
Afterward, you can apply the 1 : √3 : 2 to find the missing sides.
University of Arkansas at Monticello
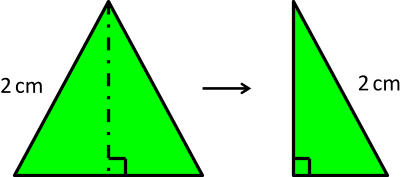
Consider an equilateral triangle with side length of 2 cm. The triangle is cut in half as shown in the figure above. What is the length of the smaller triangle’s base?
A. 1 cm
B. √2 cm
C. 1.5 cm
D. 2 cm
E. Not enough information
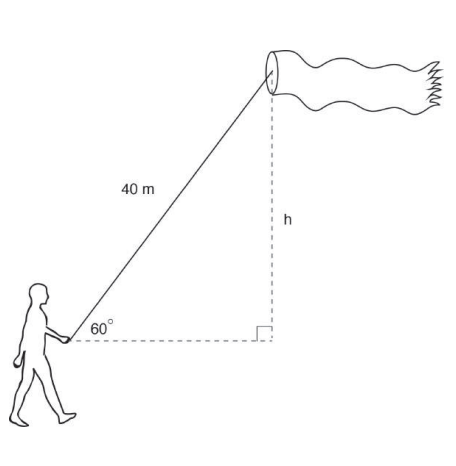
A person is flying a kite using 40 meters of kite string as shown in the diagram. What is the approximate measure of the height, h, of the kite?
Answer: h = 10 √3 m
Explanation: Find the Short Leg first by dividing the hypotenuse to 2, and then multiply the Short Leg to the square root of 3
City Tech – New York City College of Technology
Paulo is mailing an engraved plaque that is 314 inches high to the winner of a chess tournament. He has a mailer that is a triangular prism with 4-inch equilateral triangle bases as shown in the diagram. Will the plaque fit through the opening of the mailer? Explain.
Solution: If the plaque will fit, then the height of the plaque must be less than the altitude of the equilateral triangle. Draw the altitude of the equilateral triangle. Since the triangle is equilateral, the altitude will divide the triangle into two smaller congruent 30-60-90 triangles. Let x represent the length of the altitude and use the 30-60-90 Triangle Theorem to determine the value of x.
Brewton City Schools
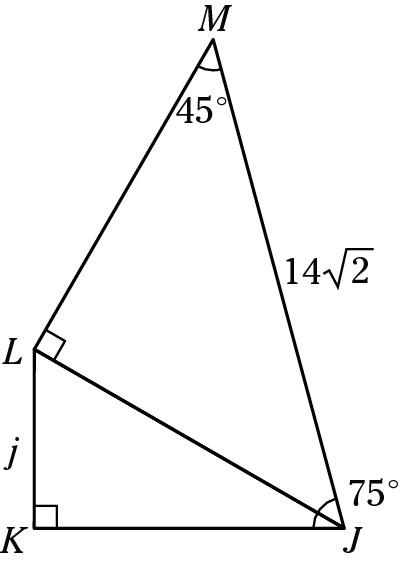
In this diagram, the measure of side j is
A. 7
B. 7√2
C. 7√3
D. 14
E. 14√2
Answer: A
Explanation: To answer this question, you must first realize that the triangles here are special; break up the 75° angle at the bottom right into a 45° angle and a 30° angle. The top right triangle is a 45-45-90 triangle, which makes both of its legs equal to 14. The bottom leg is also the hypotenuse of the 30-60-90 triangle at the bottom. In a 30-60-90 triangle, the hypotenuse must be twice the shortest leg, which is j. Therefore, j equals 7.
Don’t remember the special triangle ratios you need to know for this problem? Well, don’t panic. They’re at the top of each mathematics section of the SAT, so take a quick peek at the directions at the beginning of the section to refresh your memory
CrackSAT
Conclusion
We hope we managed to explain and discuss clearly what a 30 60 90 triangle is.
To briefly recapped, we covered
- What is a 30 60 90 triangle?
- Things you should remember
- How to solve the missing side?
- Practice Problem
We have also wrote a few articles that we thought are relevant for your grade level
- 113 Creative Writing Prompts
- Converting Celsius to Fahrenheit
- Making Sense of the Electronegativity Chart
- Density of Water
- SAT Vocabulary Words
Todd VanDuzer
Latest posts by Todd VanDuzer (see all)
- Why Finding the Right Thing to Study Matters: Setting the Foundation for Success - July 26, 2023
- How USA Staff Onboarding Benefits From Innovative Software - July 26, 2023
- Top 7 Best Reasons to Get an MBA - June 7, 2023
- How to Support Your Child When They Go to College - April 29, 2023
- How to Maximize Your Job Search with Expert Resume Writers Experienced in Your Field - April 20, 2023